Difference between revisions of "NumLib Documentation"
(→Gamma function: Update embedded images) |
(→Special functions (unit "spe"): Incomplete gamma function) |
||
| Line 54: | Line 54: | ||
The [https://en.wikipedia.org/wiki/Gamma_function gamma function] is needed by many probability functions. It is defined by the integral | The [https://en.wikipedia.org/wiki/Gamma_function gamma function] is needed by many probability functions. It is defined by the integral | ||
| − | : [[File:numlib_gamma_formula.png| | + | : [[File:numlib_gamma_formula.png|x40px]] |
NumLib provides two functions for its calculation: | NumLib provides two functions for its calculation: | ||
| Line 65: | Line 65: | ||
The second function, <code>spelga</code> calculates the natural logarithm of the gamma function which is more suitable to combinatorial calculations where multiplying and dividing the large gamma values can be avoided by adding or subtracting their logarithms. | The second function, <code>spelga</code> calculates the natural logarithm of the gamma function which is more suitable to combinatorial calculations where multiplying and dividing the large gamma values can be avoided by adding or subtracting their logarithms. | ||
| + | |||
| + | === Incomplete gamma function === | ||
| + | [[file:numlib_gammapq.png|right]] | ||
| + | The lower and upper [https://en.wikipedia.org/wiki/Incomplete_Gamma_function incomplete gamma functions] are defined by | ||
| + | |||
| + | : [[File:numlib_gammap_formula.png|x40px]] | ||
| + | : [[File:numlib_gammaq_formula.png|x40px]] | ||
| + | |||
| + | In fpc 3.2, these functions were added to NumLib for their calculation | ||
| + | <syntaxhighlight> | ||
| + | function gammap(s, x: ArbFloat): ArbFloat; | ||
| + | function gammaq(s, x: ArbFloat): ArbFloat; | ||
| + | </syntaxhighlight> | ||
== Solving linear systems of equations (unit "sle") == | == Solving linear systems of equations (unit "sle") == | ||
Revision as of 11:28, 16 April 2017
UNDER CONSTRUCTION
Introduction
Data types and declarations (unit "typ")
Finding the roots of a function (unit "roo")
The roots are the x values at which a function f(x) is zero.
Bisection
In the bisection method two x values a and b are estimated to be around the expected root such that the function values have opposite signs at a and b. The center point of the interval is determined, and the subinterval for which the function has opposite signs at its endpoints is selected for a new iteration. The process ends when a given precision, i.e. interval length, is achieved.
In NumLib, this approach is supported by the procedure roof1r:
procedure roof1r(f: rfunc1r; a, b, ae, re: ArbFloat; var x: ArbFloat; var term: ArbInt);fis the function for which the root is to be determined. It must be a function of one floating point argument (typeArbFloat). The type of the function,rfunc1r, is declared in unittyp.aandbare the endpoints of the test interval. The root must be located between these two values, i. e. the function values f(a) and f(b) must have different signs.aeandredetermine the absolute and relative precision, respectively, with which the root will be determined.reis relative to the maximum of abs(a) and abs(b). Note that precision and speed are conflicting issues. Highest accuracy is achieved ifaeis given asMachEps(see unittyp). Both parameters must not be negative.xreturns the value of the found root.termreturns whether the process has been successful:- 1 - successful termination, a zero point has been found with absolute accuracy
aeor relative accuracyre - 2 - the required accuracy of the root could not be reached; However, the value of x is called the "best achievable" approach
- 3 - error in input parameters:
ae< 0 orre< 0, or f(a)*f(b) > 0
- 1 - successful termination, a zero point has been found with absolute accuracy
Example
The following program determines the square root of 2. This is the x value at which the function f(x) = x^2 - 2 is zero. Since f(1) = 1^2 - 2 = -1 < 0 and f(2) = 2^2 - 2 = 2 > 0 we can assume a and b to be 1 and 2, respectively.
program bisection_demo;
uses
typ, roo;
function f(x: ArbFloat): ArbFloat;
begin
Result := x*x - 2;
end;
var
x: ArbFloat = 0.0;
term : ArbInt;
begin
roof1r(@f, 1.0, 2.0, 1e-9, 0, x, term);
WriteLn('Bisection result ', x);
WriteLn('sqrt(2) ', sqrt(2.0));
end.Special functions (unit "spe")
Gamma function
The gamma function is needed by many probability functions. It is defined by the integral
NumLib provides two functions for its calculation:
function spegam(x: ArbFloat): ArbFloat;
function spelga(x: ArbFloat): ArbFloat;The first one, spegam, calculates the function directly. But since the gamma function grows rapidly for even not-too large arguments this calculation very easily overflows.
The second function, spelga calculates the natural logarithm of the gamma function which is more suitable to combinatorial calculations where multiplying and dividing the large gamma values can be avoided by adding or subtracting their logarithms.
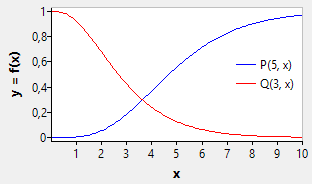
Incomplete gamma function
The lower and upper incomplete gamma functions are defined by
In fpc 3.2, these functions were added to NumLib for their calculation
function gammap(s, x: ArbFloat): ArbFloat;
function gammaq(s, x: ArbFloat): ArbFloat;