NumLib Documentation
UNDER CONSTRUCTION
Introduction
NumLib is a colletion of routines for numerical mathematics. It was written by C.J.J.M. van Ginneken, W.J.P.M. Kortsmit, and L. Reij at the Technical University of Einhoven (Netherlands) and donated to the Free Pascal project. Its beginnings date back to 1965. Originally written in Algol 60, ported to poorly formatted Pascal with strange procedure names, it is hard stuff, in particular because an official documentation is not readily available (well... -- Dutch documentation files in TeX can be found at http://www.stack.nl/~marcov/numlib/).
But after all, this library contains a series of very useful routines:
- Calculation of special functions
- Solution of systems of linear equations
- Finding roots of equations
- Fitting routines
- Matrix inversion
- Calculation of Eigen values
Therefore, it is the intention of this wiki article to create some useful documentation. Each routine described here was tested and its description will be accompanied by a working code example.
Data types and declarations (unit typ)
Basic floating point type, ArbFloat
In NumLib, a new type ArbFloat is defined which is used as floating point type throughout the entire library. This allows to switch between IEEE Double (64bit) and Extended(80bit) (though big endian state is unknown at present).
At the time of this writing the Define ArbExtended is enabled, and therefore ArbFloat is the type extended.
In order to change the floating point type define or undefine ArbExtended and add the machineconstants change to the type selected.
Basic integer type, ArbInt
Because in plain FPC mode the type Integer is 16-bits (for TP compatibility), and in Delphi 32-bits, all integers were changed to ArbInt. The basic idea is the same as with ArbFloat.
Vectors
NumLib often passes vectors to procedures as one ArbFloat plus some integer value. This ArbFloat value is the first value of an array containing the vector, the integer is the count of elements used from this array. Internally an array type is mapped over the first value in order to access the other array elements. This way both 0- and 1-based arrays as well as static and dynamic arrays can be passed to the functions and procedures of NumLib.
procedure DoSomething(var AVector: ArbFloat; n: Integer);
type
TLocalVector = array[0..MaxElements] of ArbFloat;
var
i: Integer;
x: TLocalVector absolute AVector;
begin
for i:=0 to n-1 do
// do something with x[i]
end;
var
x: array[1..100]; // Note: This array begins with index 1!
...
DoSomething(x[1], 100);
Matrices
A matrix is a two-dimensional arrangement of numbers in m rows and n columns.
- [math]\displaystyle{ {A} = \left[ \begin{array}{cccc} a_{11} & a_{12} & a_{13} & \ldots & a_{1n}\\ a_{21} & a_{22} & a_{23} & \ldots & a_{2n}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & a_{m3} & \ldots & a_{mn} \end{array} \right] }[/math]
The matrix elements aij are addressed by row and column indexes, i and j, respectively. In mathematics, the index values usually start with 1 (i = 1..m, j = 1..n) while in computing the first index is preferred to be 0 (i = 0...m-1, j = 0...n-1).
Generic matrices
In this type of matrix, no assumption is made on symmetry and shape of the data arrangement.
A constant (real) matrix can be declared in Pascal as a two-dimensional array of floating point numbers: A: array[1..m, 1..n] of ArbFloat (or A: array[0..m-1, 0..n-1] of ArbFloat in 0-based index notation). Similarly, a constant complex matrix can be declared as an array[1..m, 1..n] of complex.
When a NumLib procedure needs a matrix the first (top left) matrix element must be passed as a var parameter, along with the number of rows and columns. It is even possible to allocate larger arrays as needed, and in this case the allocated row length (or number of columns) must be specified.
Alternatively a matrix also can be specified as a one-dimensional array. This works because all data are found within the same memory block. The array index, k must be converted to the 2D matrix indexes, i, j:
k := i * n + j <==> i = k div n, j := k mod n {for 0-based array and matrix indexes}
k := (i-1) * n + j <==> i := (k-1) div n + 1, j := (k-1) mod n + 1 {for 1-based array and matrix indexes}
Using a one-dimensional array is also the correct way to dynamically allocate memory for a matrix. The first idea of using an array of array of ArbFloat will not work because this does not allocate a single memory block. Instead, individual memory blocks will be allocated for the inner array (rows), and these pointers will be stored in the outer array - this way of storing 2D data is not compatible with the requirements of NumLib.
Here is a simple example how to create, populate and read a matrix dynamically
- [math]\displaystyle{ A = \left[ \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array} \right] }[/math]
var
A: array of Arbfloat; // Note: the index in a dynamic array is 0-based.
ij: Integer;
i, j: Integer;
p: ^ArbFloat;
m, n: Integer;
begin
m := 2;
n := 3;
SetLength(A, m, n);
A[0] := 1; A[1] := 2; A[2] := 3;
A[3] := 4; A[4] := 5; A[5] := 6;
for i := 0 to m-1 do begin
for j := 0 to n-1 do begin
ij := i * n + j;
Write(A[ij]);
end;
WriteLn;
end;
// or
p := @A[0]; // pointer to first array element
for i:=0 to m - 1 do begin
for j := 0 to n - 1 do begin
WriteLn(p^);
inc(p); // advance pointer to next array element
end;
WriteLn;
end;Tridiagonal matrices
A tridiagonal matrix has non-zero elements only along the diagonal and immediately above and below the main diagonal. This way the matrix can be stored more efficiently than a generic matrix because all the empty elements can be dropped. The elements of an n x n square tridiagonal matrix can be stored as three vectors
- an array
lwithn-1elements for the subdiagonal - an array
dwithnelements for the main diagonal, and - an array
uwithn-1elements for the superdiagonal
- [math]\displaystyle{ A= \begin{bmatrix} d[0] & u[0] & & \dots & 0 \\ l[1] & d[1] & u[1] & & \\ & l[2] & d[2] & u[2] & \\ \vdots & & \ddots & \ddots & \ddots \\ & & l[n-1] & d[n-1] & u[n-1] \\ 0 & & & l[n] & d[n] \end{bmatrix} }[/math]
Symmetric tridiagonal matrices
In these tridiagonal matrices, the subdiagonal and superdiagonal elements are equal. Consequently, NumLib requests only two, instead of three, one-dimensional arrays:
- an array
dwithnelements for the main diagonal, and - an array
cwithn-1elements for the superdiagonal and subdiagonal
- [math]\displaystyle{ A= \begin{bmatrix} d[0] & c[1] & & \dots & 0 \\ c[1] & d[1] & c[2] & & \\ & c[2] & d[2] & c[3] & \\ \vdots & & \ddots & \ddots & \ddots \\ & & c[n-1] & d[n-1] & c[n] \\ 0 & & & c[n] & d[n] \end{bmatrix} }[/math]
Complex numbers
NumLib defines the type complex as a TP object. Real and imaginary parts are denoted as xreal and imag, respectively. Methods for basic operations are provided:
type
complex = object
xreal, imag : ArbFloat;
procedure Init(r, i: ArbFloat); // Initializes the number with real and imaginary parts r and i, resp
procedure Add(c: complex); // Adds another complex number
procedure Sub(c: complex); // Subtracts a complex number
function Inp(z:complex):ArbFloat; // Calculates the inner product (a.Re * b.Re + a.Im * b.Im)
procedure Conjugate; // Conjugates the value (i.e. negates the imaginary part)
procedure Scale(s: ArbFloat); // Multiplies real and imaginary part by the real value s
function Norm: ArbFloat; // Calculates the "norm", i.e. sqr(Re) + sqr(Im)
function Size: ArbFloat; // Size = sqrt(Norm)
function Re: ArbFloat; // Returns the real part of the complex number
procedure Unary; // Negates real and imaginary parts
function Im: ArbFloat; // Returns the imaginary part of the complex number
function Arg: ArbFloat; // Calculates the phase phi of the complex number z = x + y i = r exp(i phi)
procedure MinC(c: complex); // Converts itself to the minimum of real and imaginary parts
procedure MaxC(c: complex); // Converts itself to the maximum of real and imaginary ports
procedure TransF(var t: complex);
end;The real and imaginary parts of a complex number can also be retrieved by these stand-alone functions:
function Re(c: complex): ArbFloat;
function Im(c: complex): ArbFloat;
Basic operations with matrices and vectors (unit omv)
Inner product of two vectors
The result of the inner product of two vectors a = [a1, a2, ... an] and b = [b1, b2, ... bn] (also called "dot product" or "scalar product") is a scalar, i.e. a single number. It is calculated as the sum of the element-by-element products of the vectors. Both vectors must have the same lengths.
- [math]\displaystyle{ \mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^n a_i b_i = a_1 b_1 + a_2 b_2 + \dots + a_n b_n }[/math]
NumLib provides the function omvinp for calculation of the inner product:
function omvinp(var a, b: ArbFloat; n: ArbInt): ArbFloat;aandbare the first elements of 1-dimensional arrays representing the vectors a and b, respectively.ndefines the dimension of the vectors (count of array elements). Both vectors must have the same number of elements.
Example
Calculate the dot product of the vectors a = [0, 1, 2, 2, -1] and b = [3, -1, -2, 2, -1].
program dot_product;
uses
typ, omv;
const
n = 5;
a: array[0..n-1] of ArbFloat = (0, 1, 2, 2, -1);
b: array[0..n-1] of Arbfloat = (3, -1, -2, 2, -1);
var
ab: ArbFloat;
i: Integer;
begin
ab := omvinp(a[0], b[0], n);
Write('Vector a = [');
for i:= Low(a) to High(a) do
Write(a[i]:5:0);
WriteLn(' ]');
Write('Vector b = [');
for i:= Low(b) to High(b) do
Write(b[i]:5:0);
WriteLn(' ]');
Write('Dot product a b = ');
WriteLn(ab:0:0);
end.Product of two matrices
The product of a m x n matrix A and a n x p matrix B is a m x p matrix C in which the elements are calculated as the inner product of the row vectors of A and the column vectors of B (see here for more details):
- [math]\displaystyle{ C_{ij} = \sum_{k=0}^n A_{ik} B_{kj} }[/math]
The NumLib function to perform this multipication is omvmmm ("mmm" = multiply matrix by matrix):
procedure omvmmm(var a: ArbFloat; m, n, rwa: ArbInt;
var b: ArbFloat; p, rwb: ArbInt;
var c: ArbFloat; rwc: ArbInt);ais the first element of the first input matrix A. The array will not be changed.mspecifies the number of rows (or: column length) of matrix A.nspecifies the number or columns (or: row length) of matrix A.rwais the allocated row length of matrix A. This means that the array can be allocated larger than actually needed. Of course,rwacannot be smaller thann.
bis the first element of the second input matrix B. Again, this array will not be changed.pspecifies the number or columns (or: row length) of matrix B. The number of rows is already defined by the number of columns of matrix A,n.rwbis the allocated row length of matrix B.rwbcannot be smaller thanp.
cis the first element of the output matrix C. After the calculation, this and the following array elements will contain the elements of the product matrix.- The size of the output matrix is
mrows xpcolumns as set up by the input matrices A and B. rwcis the allocated row length of matrix C.rwccannot be smaller thanp.
- The size of the output matrix is
Example
Calculate the product of the matrices
- [math]\displaystyle{ A = \begin{bmatrix} 3 & \ 5 & 4 & 1 & -4 \\ -2 & \ 3 & 4 & 1 & 0 \\ 0 & \ 1 & -1 & -2 & 5 \end{bmatrix} \ \ \ \ \ B = \begin{bmatrix} 3 & 4 & -2 & 0 \\ 0 & -2 & 2 & 1 \\ -1 & 0 & 3 & 4 \\ -2 & -3 & 0 & 1 \\ 1 & 3 & 0 & -1 \end{bmatrix} }[/math]
program matrix_multiplication;
uses
typ, omv;
const
m = 3;
n = 5;
p = 4;
A: array[1..m, 1..n] of ArbFloat = (
( 3, 5, 4, 1, -4),
(-2, 3, 4, 1, 0),
( 0, 1, -1, -2, 5)
);
B: array[1..n, 1..p] of ArbFloat = (
( 3, 4, -2, 0),
( 0, -2, 2, 1),
(-1, 0, 3, 4),
(-2, -3, 0, 1),
( 1, 3, 0, -1)
);
var
C: array[1..m, 1..p] of ArbFloat;
i, j: Integer;
begin
// Calculate product
omvmmm(
A[1,1], m, n, n,
B[1,1], p, p,
C[1,1], p
);
// Print A
WriteLn('A = ');
for i:= 1 to m do begin
for j := 1 to n do
Write(A[i, j]:10:0);
WriteLn;
end;
WriteLn;
// Print B
WriteLn('B = ');
for i:= 1 to n do begin
for j := 1 to p do
Write(B[i, j]:10:0);
WriteLn;
end;
WriteLn;
// Print C
WriteLn('C = A B = ');
for i:= 1 to m do begin
for j := 1 to p do
Write(C[i, j]:10:0);
WriteLn;
end;
end.
Product of a matrix with a vector
A matrix A of size m x n multiplied with a vector b of length n yields another vector of length m. The elements of the result vector c are the dot products of the matrix rows with b. Note that the length of vector b must be equal to the number of columns of matrix A.
- [math]\displaystyle{ \begin{align*} \mathbf{c} = A\ \mathbf{b}= \left[ \begin{array}{cccc} a_{11} & a_{12} & a_{13} & \ldots & a_{1n}\\ a_{21} & a_{22} & a_{23} & \ldots & a_{2n}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & a_{m3} & \ldots & a_{mn} \end{array} \right] \ \ \left[ \begin{array}{c} b_1\\ b_2\\ b_3\\ \vdots\\ b_n \end{array} \right] = \left[ \begin{array}{c} a_{11}b_1+a_{12}b_2 + a_{13}b_3 + \cdots + a_{1n} b_n\\ a_{21}b_1+a_{22}b_2 + a_{23}b_3 + \cdots + a_{2n} b_n\\ \vdots\\ a_{m1}b_1+a_{m2}b_2 + a_{m3}b_3 + \cdots + a_{mn} b_n\\ \end{array} \right]. \end{align*} }[/math]
NumLib's procedure for this task is called omvmmv ("mmv" = multiply a matrix with a vector):
procedure omvmmv(var a: ArbFloat; m, n, rwidth: ArbInt; var b, c: ArbFloat);
Example
Calculate the product
- [math]\displaystyle{ \begin{align*} \mathbf{c} = A\ \mathbf{b}= \left[ \begin{array}{cccc} 3 & 5 & 4 & 1 & -4\\ -2 & 3 & 4 & 1 & 0\\ 0 & 1 & -1 & -2 & 5 \end{array} \right] \ \ \left[ \begin{array}{c} 3\\ 0\\ -1\\ -2\\ 1 \end{array} \right] \end{align*} }[/math]
program matrix_vector_multiplication;
uses
typ, omv;
const
m = 3;
n = 5;
p = 4;
A: array[1..m, 1..n] of ArbFloat = (
( 3, 5, 4, 1, -4),
(-2, 3, 4, 1, 0),
( 0, 1, -1, -2, 5)
);
b: array[1..n] of ArbFloat = (
3, 0, -1, -2, 1
);
var
c: array[1..m] of ArbFloat;
i, j: Integer;
begin
// Calculate product c = A b
omvmmv(
A[1,1], m, n, n,
b[1],
c[1]
);
// Print A
WriteLn('A = ');
for i:= 1 to m do begin
for j := 1 to n do
Write(A[i, j]:10:0);
WriteLn;
end;
WriteLn;
// Print vector b
WriteLn('b = ');
for i:= 1 to n do
Write(b[i]:10:0);
WriteLn;
WriteLn;
// Print result vector c
WriteLn('c = A b = ');
for i:= 1 to m do
Write(c[i]:10:0);
WriteLn;
end.Transpose matrix
The transpose matrix AT of matrix A is obtained by flipping rows and columns:
- [math]\displaystyle{ \begin{align*} {A} = \left[ \begin{array}{cccc} a_{11} & a_{12} & a_{13} & \ldots & a_{1n}\\ a_{21} & a_{22} & a_{23} & \ldots & a_{2n}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & a_{m3} & \ldots & a_{mn} \end{array} \right] \ \ \ {A^T} = \left[ \begin{array}{cccc} a_{11} & a_{21} & \ldots & a_{m1}\\ a_{12} & a_{22} & \ldots & a_{m2}\\ a_{13} & a_{23} & \ldots & a_{m3} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \ldots & a{mn} \end{array} \right] \end{align*} }[/math]
Use the procedure omvtrm to perform this operation with NumLib:
procedure omvtrm(
var a: ArbFloat; m, n, rwa: ArbInt;
var c: ArbFloat; rwc: ArbInt
);adenotes the first element of the input matrix A. The elements of this array are not changed by the procedure.mis the number of rows of matrix A.nis the number of columns of matrix A.rwais the number of allocated columns of A. This way the array of A can be larger than acutally needed.
cis the first element of the transposed matrix AT. It hasnrows andmcolumns.rwcis the number of allocated columns for the transposed matrix.
Example
Obtain the transpose of the 2x4 matrix
- [math]\displaystyle{ {A} = \left[ \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 11 & 22 & 33 & 44 \end{array} \right] }[/math]
program transpose;
uses
typ, omv;
const
m = 2;
n = 4;
A: array[1..m, 1..n] of ArbFloat = (
( 1, 2, 3, 4),
(11, 22, 33, 44)
);
var
C: array[1..n, 1..m] of ArbFloat;
i, j: Integer;
begin
// Transpose A
omvtrm(
A[1,1], m, n, n,
C[1,1], m
);
// Print A
WriteLn('A = ');
for i:= 1 to m do begin
for j := 1 to n do
Write(A[i, j]:10:0);
WriteLn;
end;
WriteLn;
// Print C
WriteLn('AT = ');
for i:= 1 to n do begin
for j := 1 to m do
Write(C[i, j]:10:0);
WriteLn;
end;
end.
Norm of vectors and matrices
A norm is a function which assigns a positive "length" to a vector a or a matrix M.
In case of vectors, NumLib supports these norms:
- The 1-norm of a vector is defined as the sum of the absolute values of the vector components. It is also called "Taxicab" or "Manhattan" norm because it corresponds to the distance that a taxis has to drive in a rectangular grid of streets.
- [math]\displaystyle{ \|a\|_1 = \sum_{i=1}^n |{a_i}| }[/math]
- The 2-norm (also: Euclidian norm) corresponds to the distance of point a from the origin.
- [math]\displaystyle{ \|a\|_2 = \sqrt{\sum_{i=1}^n {a_i}^2} }[/math]
- The maximum infinite norm of a vector is the maximum absolute value of its components.
- [math]\displaystyle{ \|a\|_\infty = \max({a_1}, {a_2}, ... {a_n}) }[/math]
The norms of matrices, as implemented by NumLib, are usually defined by row or column vectors:
- The 1-norm of a matrix is the maximum of the absolute column sums:
- [math]\displaystyle{ \|M\|_1 = \max_{1 \le j \le {n}} \sum_{i=1}^m|M_{ij}| }[/math]
- The maximum infinite norm of a matrix is the maximum of the absolute row sum.
- [math]\displaystyle{ \|M\|_\infty = \max_{1 \le i \le\ m} \sum_{j=1}^n |M_{ij}| }[/math]
- Only the Frobenius norm is calculated by individual matrix elements. It corresponds to the 2-norm of vectors, only the sum runs over all matrix elements:
- [math]\displaystyle{ \|M\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n {M_{ij}}^2} }[/math]
These are the NumLib procedure for calculation of norms:
function omvn1v(var a: ArbFloat; n: ArbInt): ArbFloat; // 1-norm of a vector
function omvn1m(var a: ArbFloat; m, n, rwidth: ArbInt): ArbFloat; // 1-norm of a matrix
function omvn2v(var a: ArbFloat; n: ArbInt): ArbFloat; // 2-norm of a vector
function omvnfm(Var a: ArbFloat; m, n, rwidth: ArbInt): ArbFloat; // Frobenius norm of a matrix
function omvnmv(var a: ArbFloat; n: ArbInt): ArbFloat; // Maximum infinite norm of a vector
function omvnmm(var a: ArbFloat; m, n, rwidth: ArbInt): ArbFloat; // Maximum infinite norm of a matrixais the first element of the vector or matrix of which the norm is to be calculatedm, in case of a matrix norm, is the number of matrix rows.nis the number of vector elements in case of a vector norm, or the number of columns in case of a matrix norm.rwidth, in case of a matrix norm, is the allocated count of columns. This way a larger matrix can be allocated than actually needed.
Example
program norm;
uses
typ, omv;
const
n = 2;
m = 4;
a: array[0..m-1] of ArbFloat = (0, 1, 2, -3);
b: array[0..m-1, 0..n-1] of Arbfloat = ((3, -1), (-2, 2), (0, -1), (2, 1));
var
i, j: Integer;
begin
Write('Vector a = [');
for i:= Low(a) to High(a) do
Write(a[i]:5:0);
WriteLn(' ]');
WriteLn(' 1-norm of vector a: ', omvn1v(a[0], m):0:3);
WriteLn(' 2-norm of vector a: ', omvn2v(a[0], m):0:3);
WriteLn(' maximum norm of vector a: ', omvnmv(a[0], m):0:3);
WriteLn;
WriteLn('Matrix b = ');
for i:= 0 to m-1 do begin
for j := 0 to n-1 do
Write(b[i,j]:5:0);
WriteLn;
end;
WriteLn(' 1-norm of matrix b: ', omvn1m(b[0, 0], m, n, n):0:3);
WriteLn('Forbenius norm of matrix b: ', omvnfm(b[0, 0], m, n, n):0:3);
WriteLn(' maximum norm of matrix b: ', omvnmm(b[0, 0], m, n, n):0:3);
ReadLn;
end.
Inverse of a matrix (unit inv)
Generic matrix
Procedure invgen calculates the inverse of an arbitrary (square) nxn matrix with unknown symmetry. The calculation is based on LU decomposition with partial pivoting.
procedure invgen(n, rwidth: ArbInt; var ai: ArbFloat; var term: ArbInt);nindicates the size of the matrix.rwidthis length of the rows of the two-dimensional array which holds the matrix. Normallyn = rwidth, but the matrix could have been declared larger than actually needed; in this caserwidthrefers to the declared size of the 2D array.aiis the first (top-left) element of the matrix in the 2D array. After the calculation the input data are overwritten by the elements of the inverse matrix in case of successful completion (term = 1); in other cases, the matrix elements are undefined.termprovides an error code:- 1 - successful completion, the elements of the inverse matrix can be found at the same place as the input matrix.
- 2 - the inverse could not be calculated because the input matrix is (almost) singular.
- 3 - incorrect input data,
n < 1.
Example
Find the inverse of the matrix
- [math]\displaystyle{ A = \begin{bmatrix} 2 & 5 & 3 & 1 \\ 1 & 4 & 4 & 3 \\ 3 & 2 & 5 & 3 \\ 1 & 4 & 2 & 2 \end{bmatrix} }[/math]
program inv_general_matrix;
uses
typ, inv, omv;
const
n = 4;
D = 5;
var
// a is the input matrix to be inverted
a: array[1..n, 1..n] of ArbFloat = (
(2, 5, 3, 1),
(1, 4, 4, 3),
(3, 2, 5, 3),
(1, 4, 2, 2)
);
b: array[1..n, 1..n] of Arbfloat;
c: array[1..n, 1..n] of ArbFloat;
term: Integer = 0;
i, j: Integer;
begin
// write input matrix
WriteLn('a = ');
for i := 1 to n do begin
for j := 1 to n do
Write(a[i, j]:10:D);
WriteLn;
end;
WriteLn;
// Store input matrix because it will be overwritten by the inverse of a
for i := 1 to n do
for j := 1 to n do
b[i, j] := a[i, j];
// Calculate inverse matrix
invgen(n, n, a[1, 1], term);
// write inverse
WriteLn('a^(-1) = ');
for i := 1 to n do begin
for j := 1 to n do
Write(a[i, j]:10:D);
WriteLn;
end;
WriteLn;
// Check validity of result by multiplying inverse with saved input matrix
omvmmm(a[1, 1], n, n, n, // "mmm" = Multiply Matrix with Matrix
b[1, 1], n, n,
c[1, 1], n);
// write inverse
WriteLn('a^(-1) x a = ');
for i := 1 to n do begin
for j := 1 to n do
Write(c[i, j]:10:D);
WriteLn;
end;
end.Determinant of a matrix (unit det)
Unit det provides a series of routines for calculation of the determinant of a square matrix. Besides a procedure for general matrices there are also routines optimized for special matrix types (tridiagonal, symmetric).
In order to avoid possible overflows and underflows a factor may be split off during calculation, and the determinant is returned as a floating point number f times a multiplier 8k. In many cases, however, k = 0, and the determinant simply is equal to f.
Determinant of a generic matrix
The determinant of a generic matrix is calculated by the procedure detgen:
procedure detgen(n, rwidth: ArbInt; var a, f: ArbFloat; var k, term: ArbInt);ndetermines the number of rows and columns of the input matrix (it must be square matrix).rwidthspecifies the allocated row length of the input matrix. This takes care of the fact that matrices can be allocated larger than actually needed.ais the first (i.e. top/left) element of the input matrix. The entire matrix must be contained within the same allocated memory block.fandkreturn the determinant of the matrix. The determinant is given by f * 8k. Usually k = 0, and the determinant simply is equal to f.
Example
Calculate the determinant of the 4x4 matrix
- [math]\displaystyle{ A= \left[ \begin{array}{rrrr} 4 & 2 & 4 & 1 \\ 30 & 20 & 45 & 12 \\ 20 & 15 & 36 & 10 \\ 35 & 28 & 70 & 20 \end{array} \right] }[/math]
program determinant_generic_matrix;
uses
math, typ, det;
const
n = 4;
const
a: array[1..n, 1..n] of ArbFloat = (
( 4, 2, 4, 1),
(30, 20, 45, 12),
(20, 15, 36, 10),
(35, 28, 70, 20)
);
var
f: ArbFloat;
k: Integer;
term: Integer = 0;
i, j: Integer;
begin
// write input matrix
WriteLn('A = ');
for i := 1 to n do begin
for j := 1 to n do
Write(a[i, j]:10:0);
WriteLn;
end;
WriteLn;
// Calculate determinant
detgen(n, n, a[1, 1], f, k, term);
if term = 1 then
WriteLn('Determinant of A = ', f * intpower(8, k):0:9, ' (k = ', k, ')')
else
WriteLn('Incorrect input');
end.Determinant of a tridiagonal matrix
Calculation of the determinant of a tridiagonal matrix is done by the procedure detgtr:
procedure detgtr(n: ArbInt; var l, d, u, f: ArbFloat; var k, term:ArbInt);ndenotes the number of columns and rows of the matrix (it must be square).lspecifies the first element in the subdiagonal of the matrix. This 1D array must be dimensioned to at leastn-1elements.dspecifies the first element along the main diagonal of the matrix. This 1D array must be dimensioned to contain at leastnelements.uspecifies the first element along the superdiagonal of the matrix. The array must be dimensioned to have at leastn-1elements.fandkreturn the determinant of the matrix. The determinant is given by f * 8k. Usually k = 0, and the determinant simply is equal to f.
Example
Calculate the determinant of the matrix
- [math]\displaystyle{ A= \left( \begin{array}{rrrr} 1 & 1 & & \\ 2 & 1 & 1 & \\ & 1 & 1 & 0 \\ & & 1 & 2 \end{array} \right) }[/math]
program determinant_tridiagonal_matrix;
{$mode objfpc}{$H+}
uses
math, typ, det;
const
n = 4;
const
u: array[0..n-2] of ArbFloat = (-1, -1, -1 ); // superdiagonal
d: array[0..n-1] of ArbFloat = ( 2, 2, 2, 2); // main diagonal
l: array[1..n-1] of ArbFloat = ( -1, -1, -1); // subdiagonal
var
f: ArbFloat;
k: Integer;
term: Integer = 0;
i, j: Integer;
begin
// write input matrix
WriteLn('A = ');
for i := 0 to n-1 do begin
for j := 0 to i-2 do
Write(0.0:5:0);
if i > 0 then
Write(l[i]:5:0);
Write(d[i]:5:0);
if i < n-1 then
Write(u[i]:5:0);
for j:=i+2 to n-1 do
Write(0.0:5:0);
WriteLn;
end;
WriteLn;
// Calculate determinant
detgtr(n, l[1], d[0], u[0], f, k, term);
if term = 1 then
WriteLn('Determinant of A = ', f * intpower(8, k):0:9, ' (k = ', k, ')')
else
WriteLn('Incorrect input');
ReadLn;
end.Solving systems of linear equations (unit sle)
A system of linear equations (or linear system) is a collection of two or more linear equations involving the same set of variables, x1 ... xn.
- [math]\displaystyle{ \begin{cases} a_{11} x_1 + a_{12} x_2 + \dots + a_{1n} x_n = b_1 \\ a_{21} x_1 + a_{22} x_2 + \dots + a_{2n} x_n = b_n \\ \ \ \ \vdots \\ a_{m1} x_1 + a_{m2} x_2 + \dots + a_{mn} x_n = b_m \end{cases} }[/math]
In order to find a solution which satisfies all equations simultaneously the system of equations is usually converted to a matrix equation A x = b, where
- [math]\displaystyle{ A = \left [ \begin{array}{ccc} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{array} \right ], \ \mathbf{x} = \left [ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right ], \ \mathbf{b} = \left [ \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_m \end{array} \right ] }[/math]
NumLib offers several procedures to solve the matrix equation depending on the properties of the matrix.
Generic matrix
The most general procedure is slegen. It poses the only requirement that the coefficient matrix A is square.
procedure slegen(n, rwidth: ArbInt; var a, b, x, ca: ArbFloat; var term: ArbInt);nis the number of unknown variables. It must be the same as the number of columns and rows of the coefficent matrix.rwidthidentifies the allocated number of columns of the coefficient matrix. This is useful if the matrix is allocated larger than needed. It is required thatn <= rwidth.ais the first (i.e. top left) element of the coefficient matrix A; the other elements must follow within the same allocated memory block. The matrix will not be changed during the calculation.bis the first element of the array containing the constant vector b. The array length at least must be equal ton. The vector will not be changed during the calculation.xis the first element of the array to receive the solution vector x. It must be allocated to contain at leastnvalues.cais a parameter to describe the accuracy of the solution.termreturns an error code:- 1 - successful completion, the solution vector x is valid
- 2 - the solution could not have been determined because the matrix is (almost) singular.
- 3 - error in input values:
n < 1.
The solution is calculated using Gauss elimination with partial pivoting.
Example
Solve this system of linear equations:
- [math]\displaystyle{ \begin{cases} 4 x_1 + 2 x_2 + 4 x_3 + x_4 = 5 \\ 30 x_1 + 20 x_2 + 45 x_3 + 12 x_4 = 43 \\ 20 x_1 + 15 x_2 + 36 x_3 + 10 x_4 = 31 \\ 35 x_1 + 28 x_2 + 70 x_3 + 20 x_4 = 57 \end{cases} \qquad \Rightarrow \qquad A= \left[ \begin{array}{rrrr} 4 & 2 & 4 & 1 \\ 30 & 20 & 45 & 12 \\ 20 & 15 & 36 & 10 \\ 35 & 28 & 70 & 20 \end{array} \right] , \; \mathbf{b} = \left[ \begin{array}{r} 5 \\ 43 \\ 31 \\ 57 \end{array} \right] }[/math]
program solve_gen;
uses
typ, sle, omv;
const
n = 4;
A: array[1..n, 1..n] of ArbFloat = (
( 4, 2, 4, 1),
(30, 20, 45, 12),
(20, 15, 36, 10),
(35, 28, 70, 20)
);
b: array[1..n] of ArbFloat = (
5, 43, 31, 57
);
var
x: array[1..n] of ArbFloat;
b_test: array[1..n] of ArbFloat;
ca: ArbFloat;
i, j: Integer;
term: Integer;
begin
WriteLn('Solve matrix system A x = b');
WriteLn;
// Print A
WriteLn('Matrix A = ');
for i:= 1 to n do begin
for j := 1 to n do
Write(A[i, j]:10:0);
WriteLn;
end;
WriteLn;
// Print b
WriteLn('Vector b = ');
for i:= 1 to n do
Write(b[i]:10:0);
WriteLn;
WriteLn;
// Solve
slegen(n, n, A[1, 1], b[1], x[1], ca, term);
if term = 1 then begin
WriteLn('Solution vector x = ');
for i:= 1 to n do
Write(x[i]:10:0);
WriteLn;
WriteLn;
// Check solution
omvmmv(A[1,1], n, n, n, x[1], b_test[1]);
WriteLn('Check result: A x = (must be equal to b)');
for i:= 1 to n do
Write(b_test[i]:10:0);
WriteLn;
end
else
WriteLn('Error');
end.Finding the roots of a function (unit roo)
The roots are the x values at which a function f(x) is zero.
Roots of the quadratic equation
The quadratic equation
- [math]\displaystyle{ {z}^2 + {p} {z} + {q} = 0 }[/math]
always has two, not necessarily different, complex roots. These solutions can be determined by the procedure rooqua.
procedure rooqua(p, q: ArbFloat; var z1, z2: complex);pandqare the (real) coefficients of the quadratic equationz1andz2return the two complex roots. See unit typ for the declaration of the typecomplex
Example
Determine the roots of the equation z2 + 2 z + 5 = 0.
program quadratic_equ;
uses
SysUtils, typ, roo;
var
z1, z2: complex;
const
SIGN: array[boolean] of string = ('+', '-');
begin
rooqua(2, 5, z1, z2);
WriteLn(Format('1st solution: %g %s %g i', [z1.re, SIGN[z1.im < 0], abs(z1.im)]));
WriteLn(Format('2nd solution: %g %s %g i', [z2.re, SIGN[z2.im < 0], abs(z2.im)]));
end.
Bisection
In the bisection method two x values a and b are estimated to be around the expected root such that the function values have opposite signs at a and b. The center point of the interval is determined, and the subinterval for which the function has opposite signs at its endpoints is selected for a new iteration. The process ends when a given precision, i.e. interval length, is achieved.
In NumLib, this approach is supported by the procedure roof1r:
procedure roof1r(f: rfunc1r; a, b, ae, re: ArbFloat; var x: ArbFloat; var term: ArbInt);fis the function for which the root is to be determined. It must be a function of one floating point argument (typeArbFloat). The type of the function,rfunc1r, is declared in unittyp.aandbare the endpoints of the test interval. The root must be located between these two values, i. e. the function values f(a) and f(b) must have different signs.aeandredetermine the absolute and relative precision, respectively, with which the root will be determined.reis relative to the maximum of abs(a) and abs(b). Note that precision and speed are conflicting issues. Highest accuracy is achieved ifaeis given asMachEps(see unittyp). Both parameters must not be negative.xreturns the value of the found root.termreturns whether the process has been successful:- 1 - successful termination, a zero point has been found with absolute accuracy
aeor relative accuracyre - 2 - the required accuracy of the root could not be reached; However, the value of x is called the "best achievable" approach
- 3 - error in input parameters:
ae< 0 orre< 0, or f(a)*f(b) > 0
- 1 - successful termination, a zero point has been found with absolute accuracy
Example
The following program determines the square root of 2. This is the x value at which the function f(x) = x^2 - 2 is zero. Since f(1) = 1^2 - 2 = -1 < 0 and f(2) = 2^2 - 2 = 2 > 0 we can assume a and b to be 1 and 2, respectively.
program bisection_demo;
uses
typ, roo;
function f(x: ArbFloat): ArbFloat;
begin
Result := x*x - 2;
end;
var
x: ArbFloat = 0.0;
term : ArbInt;
begin
roof1r(@f, 1.0, 2.0, 1e-9, 0, x, term);
WriteLn('Bisection result ', x);
WriteLn('sqrt(2) ', sqrt(2.0));
end.Numerical integration of a function (unit int)
The NumLib function int1fr calculates the integral of a given function between limits a and b with a specified absolute accuracy ae:
procedure int1fr(f: rfunc1r; a, b, ae: ArbFloat; var integral, err: ArbFloat; var term: ArbInt);fpoints to the function to be integrated. It must be a function of a single real variable (typeArbFloat) and return anArbfloat. See the typerfunc1rdeclared in unit typ.a, bare the limits of integration.aand/orbcan attain the values+/-Infinityfor integrating over an infinite interval. The order ofaandbis handled in the mathematically correct sense.aedetermines the absolute accuracy requested.integrealreturns the value of the integral. It is only valid ifterm = 1.errreturns the achieved accuracy if the specified accuracy could not be reached.termhas the value 2 in this case.termreturns an error code:- 1 - successful termination, the integral could be calculated with absolute accuracy
ae. - 2 - the requested accuracy could not be reached. But the integral is approximated within the accuracy
err. - 3 - incorrect input data:
ae < 0, ora = b = infinity, ora = b = -infinity - 4 - the integral could not be calculated: divergence, or too-slow convergence.
- 1 - successful termination, the integral could be calculated with absolute accuracy
Example
Calculate the integral
- [math]\displaystyle{ \int_a^b \frac 1 {x^2} \mathrm{d}x }[/math]
for several integration limits a and b. Since the function diverges at x = 0 the interval from a to b must not contain this point. The analytic result is [math]\displaystyle{ -1/{b} + 1/{a} }[/math]
program integrate;
uses
SysUtils, typ, int;
function recipx2(x: ArbFloat): ArbFloat;
begin
Result := 1.0 / sqr(x);
end;
function integral_recipx2(a, b: ArbFloat): Arbfloat;
begin
if a = 0 then
a := Infinity
else if a = Infinity then
a := 0.0
else
a := -1/a;
if b = 0 then
b := Infinity
else if b = Infinity then
b := 0.0
else
b := -1/b;
Result := b - a;
end;
procedure Execute(a, b: ArbFloat);
var
err: ArbFloat = 0.0;
term: ArbInt = 0;
integral: ArbFloat = 0.0;
begin
try
int1fr(@recipx2, a, b, 1e-9, integral, err, term);
except
term := 4;
end;
Write(' The integral from ' + FloatToStr(a) + ' to ' + FloatToStr(b));
case term of
1: WriteLn(' is ', integral:0:9, ', exected: ', integral_recipx2(a, b):0:9);
2: WriteLn(' is ', integral:0:9, ', error: ', err:0:9, ', exected: ', integral_recipx2(a, b):0:9);
3: WriteLn(' cannot be calculated: Error in input data');
4: WriteLn(' cannot be calculated: Divergent, or calculation converges too slowly.');
end;
end;
begin
WriteLn('Integral of f(x) = 1/x^2');
Execute(1.0, 2.0);
Execute(1.0, 1.0);
Execute(2.0, 1.0);
Execute(1.0, Infinity);
Execute(-Infinity, -1.0);
Execute(0.0, Infinity);
// NOTE: The next line will raise an exception if run in the IDE. This will not happen outside the IDE.
// Integrate(-1.0, Infinity);
end.
Special functions (unit spe)
Evaluation of a polynomial
An efficient method for evaluating a polynomial for a specific x value is Horner's scheme:
- [math]\displaystyle{ \operatorname{p}(x) = a_0 + a_1 x + a_2 x^2 + ... + a_n x^n \ \Rightarrow \ \operatorname{p}(x) = a_0 + x (a_1 + x (a_2 + \dots + x (a_{n-1} + x a_n))) }[/math]
This method is applied by NumLib's procedure spepol:
function spepol(x: ArbFloat; var a: ArbFloat; n: ArbInt): ArbFloat;xis the argument at which the polynomial is evaluated.ais the first element of an array containing the polynomial coefficients a0, a1, a2, ... an. The coefficient must be ordered from lowest to highest degree.nis the degree of the polynomial, i.e. there aren+1elements in the array.
Example
Evaluate the polynomial
- [math]\displaystyle{ \operatorname{p}(x) = 2 x^3 - 6 x^2 + 2 x - 1 }[/math]
at x = 3. Note that the terms are not in the correct order for spepol and rearrange them to
- [math]\displaystyle{ \operatorname{p}(x) = -1 + 2 x - 6 x^2 + 2 x^3 }[/math]
program polynomial;
uses
typ, spe;
const
n = 3;
a: array[0..n] of ArbFloat = (-1, 2, -6, 2);
var
x, y: ArbFloat;
begin
x := 3.0;
y := spepol(x, a[0], n);
WriteLn(y:0:6);
end.
Error function
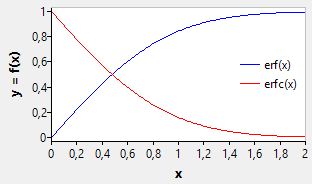
The error function erf(x) and its complement, the complementary error function erfc(x), are the lower and upper integrals of the Gaussian function, normalized to unity:
- [math]\displaystyle{ \operatorname{erf}(x) = \frac {2} {\sqrt{\pi}} \int_0^x e^{-{t}^2} dt }[/math]
- [math]\displaystyle{ \operatorname{erfc}(x) = \frac {2} {\sqrt{\pi}} \int_x^\infty e^{-{t}^2} dt = {1} - \operatorname{erf}(x) }[/math]
Both functions can be calculated by the NumLib functions speerf and speefc, respectively
function speerf(x: ArbFloat): ArbFloat; // --> erf(x)
function speefc(x: ArbFloat): ArbFloat; // --> erfc(x)
Example
A table of some values of the error function and the complementary error function is calculated in the following demo project:
program erf_Table;
uses
SysUtils, StrUtils, typ, spe;
const
Wx = 7;
Wy = 20;
D = 6;
var
i: Integer;
x: ArbFloat;
fs: TFormatSettings;
begin
fs := DefaultFormatSettings;
fs.DecimalSeparator := '.';
WriteLn('x':Wx, 'erf(x)':Wy+1, 'erfc(x)':Wy+1);
WriteLn;
for i:= 0 to 20 do begin
x := 0.1*i;
WriteLn(Format('%*.1f %*.*f %*.*f', [
Wx, x,
Wy, D, speerf(x),
Wy, D, speefc(x)
], fs));
end;
end.
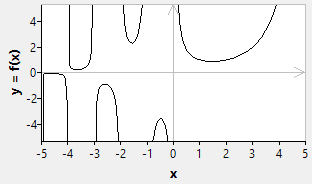
Gamma function
The gamma function is needed by many probability functions. It is defined by the integral
- [math]\displaystyle{ \Gamma({x}) = \int_0^{\infty}t^{x-1} e^{-t} dt }[/math]
NumLib provides two functions for its calculation:
function spegam(x: ArbFloat): ArbFloat;
function spelga(x: ArbFloat): ArbFloat;The first one, spegam, calculates the function directly. But since the gamma function grows rapidly for even not-too large arguments this calculation very easily overflows.
The second function, spelga calculates the natural logarithm of the gamma function which is more suitable to combinatorial calculations where multiplying and dividing the large gamma values can be avoided by adding or subtracting their logarithms.
Example
The following demo project prints a table of some values of the gamma function and of its logarithm. Note that spegam(x) overflows above about x = 170 for data type extended.
program Gamma_Table;
uses
SysUtils, StrUtils, typ, spe;
const
VALUES: array[0..2] of ArbFloat = (1, 2, 5);
Wx = 7;
Wy = 30;
Wln = 20;
var
i: Integer;
x: ArbFloat;
magnitude: ArbFloat;
begin
WriteLn('x':Wx, 'Gamma(x)':Wy, 'ln(Gamma(x))':Wln);
WriteLn;
magnitude := 1E-3;
while magnitude <= 1000 do begin
for i := 0 to High(VALUES) do begin
x := VALUES[i] * magnitude;
Write(PadLeft(FloatToStr(x), Wx));
if x <= 170 then // Extended overflow above 170
Write(FormatFloat('0.000', spegam(x)):Wy)
else
Write('overflow':Wy);
WriteLn(spelga(x):Wln:3);
if abs(x-1000) < 1E-6 then
break;
end;
magnitude := magnitude * 10;
end;
end.
Incomplete gamma function
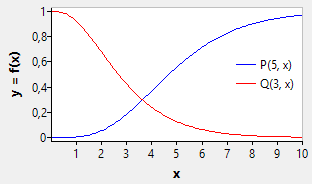
The lower and upper incomplete gamma functions are defined by
- [math]\displaystyle{ \operatorname{P}({s},{x}) = \frac{1}{\Gamma({s})} \int_0^{x}t^{s-1} e^{-t} dt }[/math]
- [math]\displaystyle{ \operatorname{Q}({s},{x}) = \frac{1}{\Gamma({s})} \int_{x}^{\infty}t^{s-1} e^{-t} dt = 1 - \operatorname{P}({s}, {x}) }[/math]
The following function have been added to NumLib in fpc 3.2 for their calculation:
function gammap(s, x: ArbFloat): ArbFloat;
function gammaq(s, x: ArbFloat): ArbFloat;
Example
The following project prints out a table of gammap and gammaq values:
program IncompleteGamma_Table;
uses
SysUtils, StrUtils, typ, spe;
const
s = 1.25;
Wx = 7;
Wy = 20;
D = 6;
var
i: Integer;
x: ArbFloat;
fs: TFormatSettings;
begin
fs := DefaultFormatSettings;
fs.DecimalSeparator := '.';
WriteLn('x':Wx, 'GammaP('+FloatToStr(s,fs)+', x)':Wy+1, 'GammaQ('+FloatToStr(s,fs)+', x)':Wy+1);
WriteLn;
for i := 0 to 20 do begin
x := 0.5*i;
WriteLn(Format('%*.1f %*.*f %*.*f', [
Wx, x,
Wy, D, gammap(s, x),
Wy, D, gammaq(s, x)
], fs));
end;
end.
Bessel functions
The Bessel functions are solutions of the Bessel differential equation:
- [math]\displaystyle{ {x}^2 y'' + x y' + ({x}^2 - \alpha^2) {y} = 0 }[/math]
The Bessel functions of the first kind, or cylindrical harmonics, Jα(x), are the solutions which are not singular at the origin, in contrast to the Bessel functions of the second kind, Yα(x). Yα(x) is only defined for x > 0.
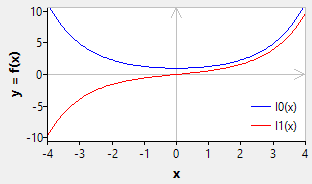
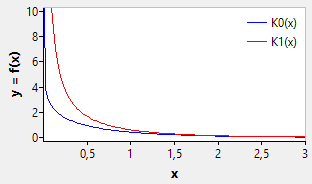
The solutions for a purely imaginary argument are called modified Bessel functions of the first kind, Iα(x), and modified Bessel function of the second kind, Kα(x). Kα(x) is only defined for x > 0.
NumLib implements only the solutions for the parameters α = 0 and α = 1:
function spebj0(x: ArbFloat): ArbFloat; // Bessel function of the first kind, J0 (alpha = 0)
function spebj1(x: ArbFloat): ArbFloat; // Bessel function of the first kind, J1 (alpha = 1)
function speby0(x: ArbFloat): ArbFloat; // Bessel function of the second kind, Y0 (alpha = 0)
function speby1(x: ArbFloat): ArbFloat; // Bessel function of the second kind, Y1 (alpha = 1)
function spebi0(x: ArbFloat): ArbFloat; // modified Bessel function of the first kind, I0 (alpha = 0)
function spebi1(x: ArbFloat): ArbFloat; // modified Bessel function of the first kind, I1 (alpha = 1)
function spebk0(x: ArbFloat): ArbFloat; // modified Bessel function of the second kind, K0 (alpha = 0)
function spebk1(x: ArbFloat): ArbFloat; // modified Bessel function of the second kind, K1 (alpha = 1)
Other functions
The unit spe contains some other functions which will not be documented here because they are already available in th FPC's standard unit math.
| Function | Equivalent function in math |
Description |
|---|---|---|
function speent(x: ArbFloat): LongInt;
|
floor(x)
|
Entier function, calculates first integer smaller than or equal to x
|
function spemax(a, b: Arbfloat): ArbFloat;
|
max(a, b)
|
Maximum of two floating point values |
function spepow(a, b: ArbFloat): ArbFloat;
|
power(a, b)
|
Calculates ab |
function spesgn(x: ArbFloat): ArbInt;
|
sign(x)
|
Returns the sign of x (-1 for x < 0, 0 for x = 0, +1 for x > 0)
|
function spears(x: ArbFloat): ArbFloat;
|
arcsin(x)
|
Inverse function of sin(x)
|
function spearc(x: ArbFloat): ArbFloat;
|
arccos(x)
|
Inverse function of cos(x)
|
function spesih(x: ArbFloat): ArbFloat;
|
sinh(x)
|
Hyperbolic sine |
function specoh(x: ArbFloat): ArbFloat;
|
cosh(x)
|
Hyperbolic cosine |
function spetah(x: ArbFloat): ArbFloat;
|
tanh(x)
|
Hyperbolic tangent |
function speash(x: ArbFloat): ArbFloat;
|
arcsinh(x)
|
Inverse of the hyperbolic sine |
function speach(x: ArbFloat): ArbFloat;
|
arccosh(x)
|
Inverse of the hyperbolic cosine |
function speath(x: ArbFloat): ArbFloat;
|
arctanh(x)
|
Inverse of the hyperbolic tangent |